Articles

Die «Lichtleitungs»-Gleichung im 12. Vortrag des Wärmekurses

Friedrich-Wilhelm Dustmann
Elemente der Naturwissenschaft 117, 2022, S. 16-42 | DOI: 10.18756/edn.117.16
Article | Sprache: German | €6.00
Artikelreferenz exportieren

Zusammenfassung:

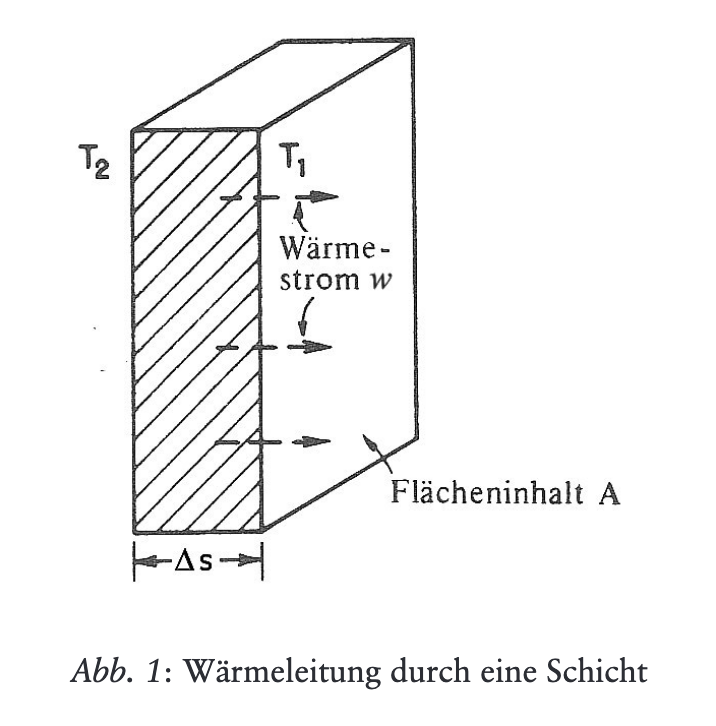
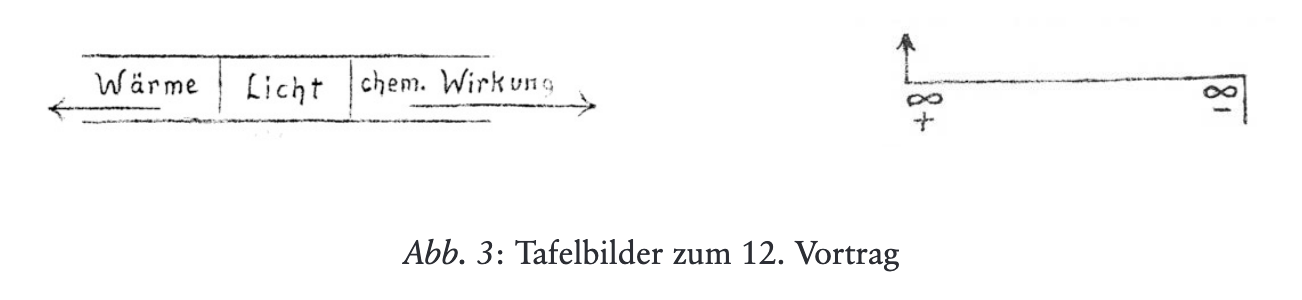
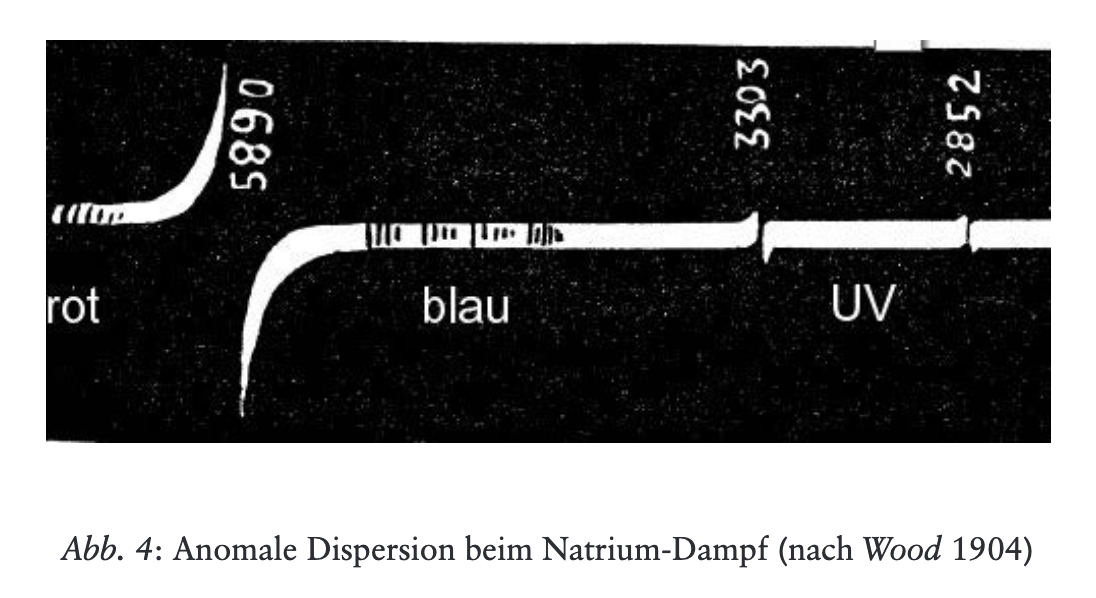
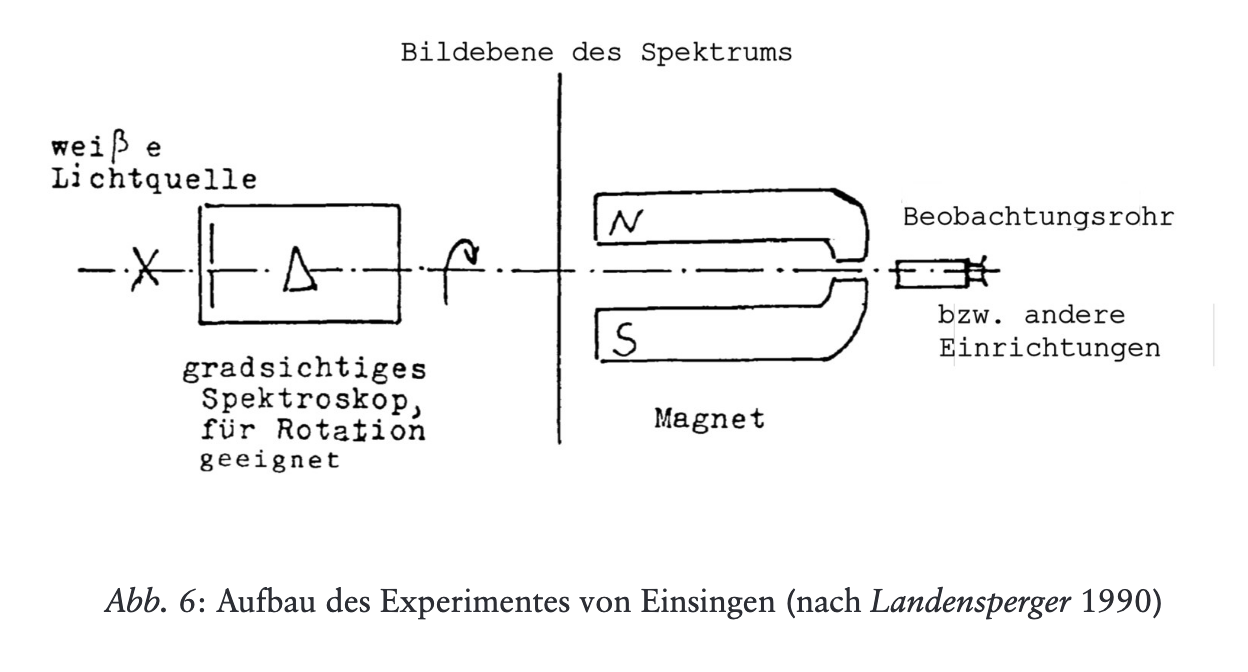
Im 12. Vortrag des Wärmekurses findet man in Anknüpfung an die Wärmeleitungsgleichung zwei weitere Differentialgleichungen, über deren Deutung und Anwendungsbereich viel gerätselt worden ist. Die letzte dieser Gleichungen soll sich auf Lichtwirkungen beziehen und zeichnet sich durch einen imaginären Koeffizienten aus, könnte also einen Diffusionsprozess mit imaginärem Diffusionskoeffizienten beschreiben. Da auch die Schrödingergleichung in diesem Sinn gedeutet werden kann, hat man die letzte Gleichung gelegentlich als eine Art Vorläufer der Schrödingergleichung gesehen. In diesem Aufsatz soll gezeigt werden, dass der Kontext, in dem sie in der Vortragsreihe steht, eine solche Deutung unwahrscheinlich macht, da es in diesem Kontext hauptsächlich um das Lichtspektrum im Zusammenhang mit Wärmewirkungen und chemischen Wirkungen geht. Es wird eine Möglichkeit aufgezeigt, wie die herkömmliche Beschreibung der Lichtausbreitung mit Hilfe der Maxwell-Gleichungen ebenfalls durch eine Differentialgleichung mit einem imaginären bzw. einem komplexen Lichtleitungskoeffzienten ausgedrückt werden kann.

Referenzen
  • Cadène, A., Berceau, P., Fouché, M., Battesti, R., Rizzo, C. (2013): Vacuum magnetic linear birefringence using pulsed fields: the BMV experiment. https://hal.archives-ouvertes.fr/hal-00793105v1
  • Dreher, E. (1882): Beiträge zu unserer modernen Atom- und Molekular-Theorie auf kritischer Grundlage. Halle.
  • Hardorp, D., Pinkall, U. (2000): Rudolf Steiner and Schrödinger’s equation, Math.-Phys. Korrespondenz 201, S. 16–22.
  • Josipovic, M. (2020): Geometric Mulriplication of Vectors – An Introduction to Geometric Algebra in Physics. Cham.
  • Kugler, W. (Hrsg.) (1987): Beiträge zur Rudolf Steiner Gesamtausgabe Nr. 95/96, Der Zwölffarbenkreis und eine Aufgabenstellung Rudolf Steiners zur Gewinnung von Lebensätherkräften aus dem Pfirsichblüt. Dornach.
  • Landensperger, W. (1990): Das Experiment von Einsingen, Elemente d. N. 52, S. 51–55.
  • Macdonald, A. (2021): Linear and Geometric Algebra. Wroclaw.
  • Pröbstl, A. (2002): Optische Aktivität von Kohlestoffverbindungen – Handeln und Erkennen im Wechsel, Elemente d. N. Sondernummer, S. 3–13.
  • Pohl, R.W. (1964): Mechanik, Akustik und Wärmelehre, 16. Aufl. Göttingen.
  • Pfeiler, W. (2017): Experimentalphysik V: Quanten, Atome, Kerne, Teilchen. Berlin, Boston.
  • Steiner, R. (1920): Zweiter Naturwissenschaftlicher Kurs, GA 321, 12. Vortrag vom 12.3.1920, 5. Auflage. Dornach, 2021.
  • Voigt, W. (1898): Doppelbrechung von im Magnetfeld befindlichen Natriumdampf in der Richtung normal zu den Kraftlinien, Nachr. Kgl. Ges. Wiss. Göttingen, S. 355–359.
  • Wood, R.W. (1904): A Quantitative Determination of Anomalous Dis- persion of Sodium Vapour in the Visible and Ultra-Violet Regions, Proceedings of the American Academy of Arts and Sciences 40, S. 365–396.